Question

I have been using a Fast Fourier Transfer (FFT) analyzer to measure the natural frequencies of my test structure. I have no problems using sine excitation. However, when I use a hammer to excite, I am seeing intermittent results. I'd suspected an issue with the accelerometer, but that was not the case. Any suggestions?

Answer

When used correctly, FFT analyzers can be powerful tools for making natural frequency determinations. They can also be used to both troubleshoot and resolve a multitude of mechanical and electrical issues.

FFT analysis is conducted on blocks, or time records, of data, with each calculation being a frequency transform of a time record of finite length. One possible cause of intermittent results when analyzing a transient (hammer) signal might be the user's choice of weighting function (or window). Let's take a look at two common weighting functions to see if this might shed some light upon the types of results that you are experiencing.

Modern FFT analyzers are equipped with a multitude of weighting functions, each designed to minimize measurement errors for a given application. For purposes of this short article, we will discuss two basic window functions, rectangular and Hanning, and briefly discuss why weighting is necessary, as well as its effects on data.



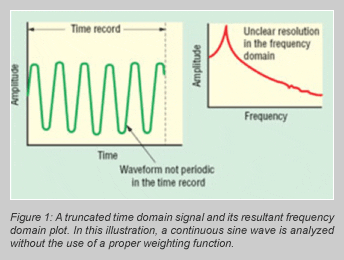
For continuous signals, problems tend to occur when the finite signal duration does not result in a sequence of whole number periods in the time record. The result is a phenomenon called spectral leakage, as illustrated in Figure 1.

Figure 2 shows the effects of applying a Hanning weighting function in the time domain and its resultant frequency domain plot. Notice the much-improved frequency resolution. The Hanning window forces the amplitude of the time record to zero at both the beginning and end of the sample interval. Since the FFT process assumes that the finite sample in the record is identical to what happens before and after the time-window, the ends of the finite record are effectively joined in a long enough loop to complete the transform. Since the Hanning weighted record is at zero at both ends, no distortion is created with the "looping" process and only the actual frequencies that are present in the signal are calculated. (It should be noted that, when calculating amplitude values from this "compressed" time domain data, the analyzer corrects for the attenuation of the weighting.) The Hanning window generator is actually amplitude modulation of the input signal, thus generating sidebands as a result of the modulation process, as shown in figure 2.



Sidebands are commonly referred to a "side lobes", though they are about -32 dB below the peak of the spectral lines and are thus of little concern. There are certain other limitations associated with use of the Hanning window, such as "picket fencing" and reduction in resolution. Details of these effects are beyond the scope of this article.

Getting back to the original question, a common error is for the new FFT analyzer user to attempt to take impulse (hammer) data with the Hanning window engaged. Referring to the time signal in Figure 2 (Time), if the impulse occurs at a time near 0 seconds (left side of the trace) or at any place other than at 50% of the time window, the signal will be completely eliminated or buried in the noise and thus no useful data will be presented in the frequency domain. Even if the impulse occurs in the center of the Hanning window, the measured amplitude will be greater than actual because of the amplitude correction applied by the analyzer.

A better choice when working with transient events, such as a hammer excitation, is to use the rectangular window. A rectangular window is actually not a window at all, which makes sense for this type of signal, as the transient event typically starts and ends at zero amplitude within the finite time length of the record. No amplitude corrections are necessary with the rectangular window, since it weights the whole event uniformly, thus ensuring good fidelity. (The rectangular window is often called "uniform weighting.") It is good practice to use triggering, if available, to be sure that all of the impulse is captured in the time record. Higher-end FFT analyzers might also have a "delay after trigger" function, such that the transient event is moved toward the center of the record, ensuring that no energy is "clipped" at the beginning of the (rectangular) window.

There are other FFT window choices available, all of which vary depending upon the analyzer manufacturer and model. As best practice, the user should review all available choices described in the product instruction manual. One example of such an additional window is the exponential window, which is worth investigation, since it will also improve the signal-to-noise ratio of the response signal.